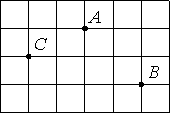
На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Площадь клетки равна 1, значит клетка имеет и единичные стороны, т.е. равные 1 (1*1=1).
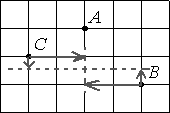Серединой отрезка BC будет будет точка, которая лежит посередине относительно вертикальной и горизонтальной осей.
То есть, относительно точки С на 2 клетки вправо и на пол клетки вниз.
Относительно точки В на две клетки влево и на пол клетки вверх.
Тогда очевидно, что расстояние от точки А до середины ВС равно 1,5
Ответ: расстояние от точки A до середины отрезка BC равно 1,5
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C прямой, BC=8, cosB=0,8. Найдите AB.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
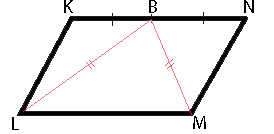В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: