
Укажите решение системы неравенств
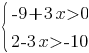
1) нет решений
2) 
3) 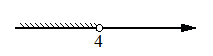
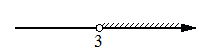
4) 
Чтобы решить систему неравенств, надо решить каждое неравенство, решением будет диапазон значений, которые удовлетворяют неравенству. И наложить диапазоны на одну ось, пересечение диапазонов и будет решением системы.
Поэтому рассмотрим каждое неравенство:
1) -9+3x>0
3x>9
x>9/3
x>3
Решением будет диапазон (3;+∞)

2) 2-3x>-10
-3x>-10-2
-3x>-12
Домножаем и правую и левую части неравенства на (-1), при этом знак неравенства меняется на противоположный (так как -1 - это отрицательное число).
3x<12
x<4
Решением будет диапазон (-∞;4)
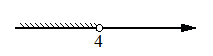
Накладываем диапазоны друг на друга:
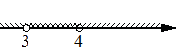
Область пересечения диапазонов (3;4) - это и будет решением системы.
Ответ: 2)
Поделитесь решением
Присоединяйтесь к нам...
Число хвойных деревьев в парке относится к числу лиственных как 4:1. Сколько процентов деревьев в парке составляют лиственные?
Решите систему уравнений 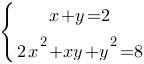
При каком значении x значения выражений 7x-2 и 3x+6 равны?
Укажите решение неравенства 4x+5≥6x-2.
1) 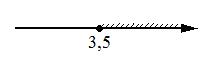
2) 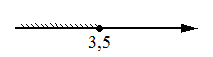
3) 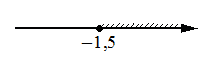
4) 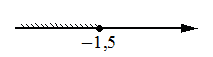
Решите уравнение x6=(5x-6)3.
Комментарии: