
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 62°. Найдите величину угла OMK. Ответ дайте в градусах.
OK перпендикулярен к
касательной (по
свойству касательной), т.е. угол между OK и
касательной равен 90°.
Следовательно, /OKM=90°-62°=28°
Треугольник OMK -
равнобедренный (т.к. OM и OK - радиусы окружности и, соответственно, равны друг другу).
По
свойству равнобедренного треугольника /OKM=/OMK=28°
Ответ: /OMK=28°
Поделитесь решением
Присоединяйтесь к нам...
 Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
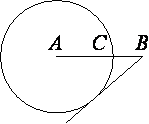 На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
 Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Комментарии: