Решите уравнение x3+5x2=9x+45.
x3+5x2=9x+45
В левой части уравнения вынесем за скобки x2:
x2(x+5)=9x+45
А в правой части вынесем 9:
x2(x+5)=9(x+5)
x2(x+5)-9(x+5)=0
Теперь вынесем за общую скобку (x+5):
(x+5)(x2-9)=0
Во второй скобке воспользуемся формулой
разность квадратов:
(x+5)(x2-32)=0
(x+5)(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю. У нас три множителя, поэтому рассмотрим 3 случая:
1) x+5=0 => x1=-5
2) x-3=0 => x2=3
3) x+3=0 => x3=-3
Ответ: x1=-5, x2=3, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
Сократите дробь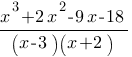 
Сократите дробь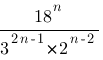 
За 10 минут велосипедист проехал a километров. За сколько минут он проедет 20 километров, если будет ехать с той же скоростью? Запишите соответствующее выражение.
Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35% золота, а во втором – 60%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?
Найдите значение выражения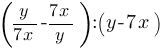 
при x=1/7, y=1/5.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: