
Решите уравнение x3+5x2-9x-45=0.
x3+5x2-9x-45=0
Из первых двух членов уравнения вынесем за скобки x2:
x2(x+5)-9x-45=0
Из остальных членов вынесем "-9":
x2(x+5)-9(x+5)=0
Теперь вынесем за общую скобку (x+5):
(x+5)(x2-9)=0
Во второй скобке воспользуемся формулой
разность квадратов:
(x+5)(x2-32)=0
(x+5)(x-3)(x+3)=0
Произведение равно нулю, когда один из множителей равен нулю. У нас три множителя, поэтому рассмотрим 3 случая:
1) x+5=0 => x1=-5
2) x-3=0 => x2=3
3) x+3=0 => x3=-3
Ответ: x1=-5, x2=3, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции 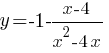
Определите, при каких значениях m прямая y=m не имеет с графиком общих точек.
Найдите значение выражения  , если √
, если √
Сократите дробь 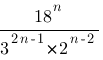
Найдите значение выражения 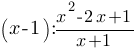 при x=-99.
при x=-99.
Найдите значение выражения 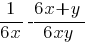 при x=√32, y=1/8.
при x=√32, y=1/8.
Комментарии: