
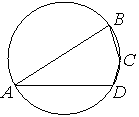 Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Угол A четырёхугольника ABCD, вписанного в окружность, равен 33°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
Так как четырехугольник вписан в окружность, то по свойству описанной окружности:
∠A+∠C=180°
∠C=180°-∠A=180°-33°=147°
Ответ: 147
Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
 Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
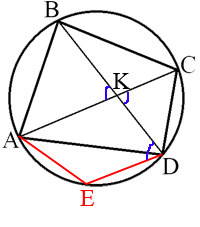 Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
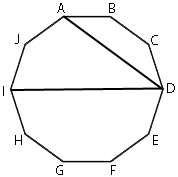 ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Комментарии: