
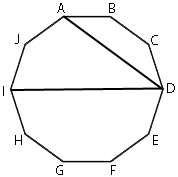
 ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
ABCDEFGHIJ – правильный десятиугольник. Найдите угол ADI. Ответ дайте в градусах.
Вариант 1 (Предложил пользователь Светлана)
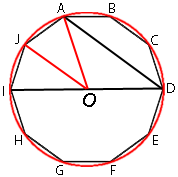 Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠AOJ) равен 360°/10=36°
Тогда ∠AOI равен:
∠AOI=36°*2=72°
∠AOI является
центральным, следовательно градусная мера дуги IJA тоже равна 76°
∠ADI тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠ADI=72°/2=36° (по
теореме о вписанном угле)
Ответ: 36
 Проведем отрезки AC и BD.
Проведем отрезки AC и BD.Поделитесь решением
Присоединяйтесь к нам...
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
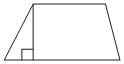 Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CKD.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
 Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром O пересекаются под углом 28°. Найдите угол ABO. Ответ дайте в градусах.
Комментарии: