
 Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
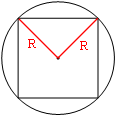 Проведем отрезки из центра
квадрата к двум его углам, как на рисунке.
Проведем отрезки из центра
квадрата к двум его углам, как на рисунке.
Заметим, что:
1) Эти отрезки и являются радиусами окружности.
2) Получившийся треугольник является
прямоугольным (по свойству квадрата).
Тогда мы можем применить
теорему Пифагора (пусть сторона квадрата - это "а"):
a2=R2+R2
a2=2R2
(40√2)2=2R2
По первому правилу действий со степенями:
402*(√2)2=2R2
402*2=2R2 |:2
402=R2
40=R
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
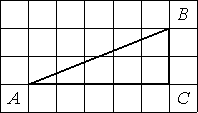 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
 В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
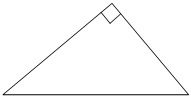 Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Комментарии: