Автор: Таська
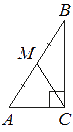
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
Так как треугольник ABC прямоугольный, то воспользуемся теоремой об описанной окружности для прямоугольного треугольника. Для этого опишем окружность вокруг треугольника ABC.
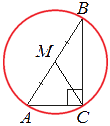Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы.
Получается, что точка М и есть центр окружности, следовательно:
R=AM=MB=AB/2=60/2=30
CM тоже является радиусом окружности, т.е.:
CM=R=30
Ответ: 30
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 32√
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
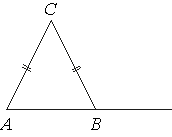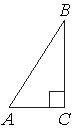В треугольнике ABC угол C прямой, AC=4, cosA=0,8. Найдите AB.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Хочу получать новые решения
Ни какого спама
Комментарии: