
Синус острого угла A треугольника ABC равен 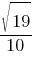 . Найдите CosA.
. Найдите CosA.
Так как нам ничего не известно про треугольник ABC, прямоугольный он или нет и т.д. То остается только воспользоваться основной тригонометрической формулой:
sin2A+cos2A=1
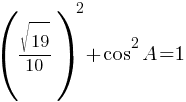
По второму правилу действий со степенями:
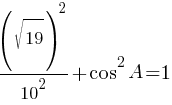
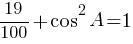
0,19+cos2A=1
cos2A=1-0,19
cos2A=0,81
cosA=√0,81=0,9
Ответ: 0,9
Поделитесь решением
Присоединяйтесь к нам...
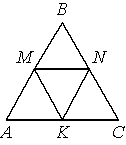 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Стороны AC, AB, BC треугольника ABC равны 2√
 Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Комментарии: