В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
По
теореме косинусов:
AC2=AB2+BC2-2*AB*BC*cos∠ABC
42=22+32-2*2*3*cos∠ABC
16=4+9-12cos∠ABC
16-4-9=-12cos∠ABC
3=-12cos∠ABC
cos∠ABC=3/(-12)=-1/4=-0,25
Ответ: -0,25
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
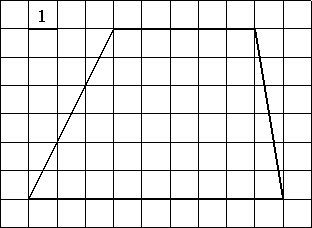Найдите площадь трапеции, изображённой на рисунке.
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина – 96 см. Найдите расстояние между точками A и B (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: