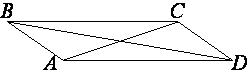
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
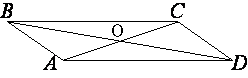Обозначим точку пересечения диагоналей как О.
По
свойству
параллелограмма AO=OC=AC/2.
AB=CD (по
другому свойству).
А так как AC в 2 раза больше стороны AB (по условию задачи), то OC=AB=CD.
Следовательно треугольник OCD -
равнобедренный.
По
свойству равнобедренного треугольника ∠COD=∠CDO.
По
теореме о сумме углов треугольника: 180°=∠COD+∠CDO+∠ACD=∠COD+∠CDO+169°
∠COD+∠CDO=11°, а так как ∠COD=∠CDO (это мы выяснили ранее), то ∠COD=∠CDO=11°/2=5,5°
∠COD - острый угол между диагоналями.
Следовательно,
∠COB=180°-∠COD=180°-5,5°=174,5° (т.к. это
смежные углы) - тупой угол между диагоналями.
Ответ: острый угол между диагоналями параллелограмма (∠COD) равен 5,5°, тупой угол между диагоналями равен 174,5°
Поделитесь решением
Присоединяйтесь к нам...
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 7°. Найдите величину угла OMK. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: