Стороны AC, AB, BC треугольника ABC равны 2√
По условию задачи /KAC>90°, т.е. это наибольший угол в треугольнике AKC следовательно, сторона KC, противолежащая этому углу тоже наибольшая (по теореме о соотношениях между сторонами и углами треугольника). Сторона AC равная 2√
По условию задачи треугольник KAC подобен исходному треугольнику ABC. А значит углы этих треугольников соответственно равны (по определению подобных треугольников). Поэтому наибольшие углы двух рассматриваемых треугольников равны, т.е. /KAC=/ABC. /ACK не равен /ACB ( т.к. KC пересекает сторону AB в точке, отличной от B), поэтому /ACK = /BAC. Следовательно, /AKC=/ACB => cos(/AKC)=cos(/ACB).
Применяя теорему косинусов мы можем записать AB2=AC2+BC2-2*AC*BC*cos(/ACB).
(√
6=4*2+1-4*√
6-9=-4*√
3=4*√
cos(/AKC)=cos(/ACB)=3/(4*√
Ответ: cos(/AKC)=3/(4*√
Поделитесь решением
Присоединяйтесь к нам...
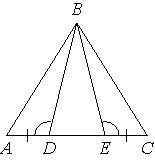На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
AC и BD – диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
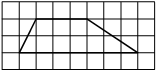На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: