
Укажите неравенство, которое не имеет решений.
1) x2+64<0
2) x2+64>0
3) x2-64>0
4) x2-64<0
Рассмотрим каждое неравенство:
1) x2+64<0
x2<-64
Квадрат любого числа является числом положительным, следовательно, ни при каких x x2 не может быть меньше отрицательного числа. Поэтому данное неравенство не имеет решений.
2) x2+64>0
x2>-64
Как говорилось ранее, x2 - число положительное, следовательно, для любого x это неравенство верно. Т.е. решение данного неравенства x⊂(-∞;+∞)
3) x2-64>0
x2>64
Очевидно, что найдутся такие x, что x2>64 (например x=100). Следовательно, данное неравенство имеет решения.
4) x2-64<0
x2<64
Очевидно, что найдутся такие x, что x2<64 (например x=1). Следовательно, данное неравенство имеет решения.
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение -3x2+4x-7=-x2+5x-(-1+2x2).
Решите уравнение x2-144=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Решите неравенство 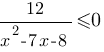
Решите уравнение 6/(x-8)=8/(x-6).
Решите уравнение (x+1)2+(x-6)2=2x2.
Комментарии:
(2017-02-26 17:14:05) Администратор: Маркус, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-02-26 11:07:15) Маркус: Укажите неравенство решением которого является любое число. кореньx^2+2x+1>0