
 AC и BD – диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD – диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.
Рассмотри треугольник OCB.
OB=OC (т.к. это радиусы)
Следовательно, треугольник OCB -
равнобедренный.
Тогда ∠ACB=∠CBD=74° (по
свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠ACB+∠CBD+∠BOC
180°=74°+74°+∠BOC
∠BOC=32°
∠BOC=∠AOD=32° (т.к. они
вертикальные).
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
 Площадь прямоугольного треугольника равна 8√
Площадь прямоугольного треугольника равна 8√
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
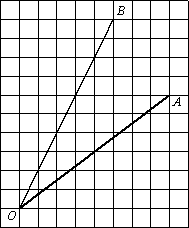 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Комментарии: