
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ482 –Є–Ј 1087 |
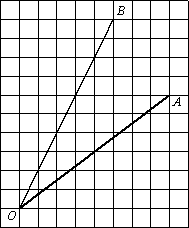 –Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ AOB.
–Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ AOB.
–Т–∞—А–Є–∞–љ—В вДЦ1 (–Я—А–Є—Б–ї–∞–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Х–≤–≥–µ–љ–Є–є)
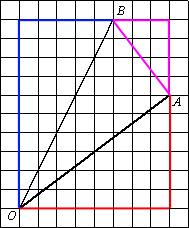 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AB.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AB.
–Э–∞–є–і–µ–Љ –Ї–∞–ґ–і—Г—О —Б—В–Њ—А–Њ–љ—Г —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABO –њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
AO2=82+62
AO2=64+36=100
AO=10
AB2=42+32
AB2=16+9=25
AB=5
BO2=102+52
BO2=100+25=125
BO=√
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤:
AB2=AO2+BO2-2AO*BO*cos∠AOB
52=102+(5√
25=100+125-2*10*5√
-200=-100√
cos∠AOB=2/√
–Я–Њ –Њ—Б–љ–Њ–≤–љ–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Д–Њ—А–Љ—Г–ї–µ:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+4/5=1
sin2∠AOB=1/5
sin∠AOB=1/√
tg∠AOB=sin∠AOB/cos∠AOB=(1/√
–Ю—В–≤–µ—В: tg∠AOB=0,5
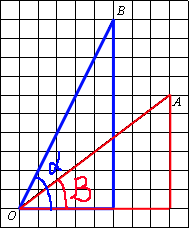 –Ф–Њ—Б—В—А–Њ–Є–Љ —З–µ—А—В–µ–ґ –і–Њ –і–≤—Г—Е
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Э–∞–є–і–µ–Љ
—В–∞–љ–≥–µ–љ—Б—Л –і–ї—П –Њ–±–Њ–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –і–ї—П –Є—Е —Г–≥–ї–Њ–≤ –Ю.
–Ф–Њ—Б—В—А–Њ–Є–Љ —З–µ—А—В–µ–ґ –і–Њ –і–≤—Г—Е
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Э–∞–є–і–µ–Љ
—В–∞–љ–≥–µ–љ—Б—Л –і–ї—П –Њ–±–Њ–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –і–ї—П –Є—Е —Г–≥–ї–Њ–≤ –Ю.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–Ъ–∞–Ї–Є–µ –Є–Ј –і–∞–љ–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ—Л? –Ч–∞–њ–Є—И–Є—В–µ –Є—Е –љ–Њ–Љ–µ—А–∞.
1) –Х—Б–ї–Є –њ—А–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є–Є –і–≤—Г—Е –њ—А—П–Љ—Л—Е —В—А–µ—В—М–µ–є –њ—А—П–Љ–Њ–є –≤–љ—Г—В—А–µ–љ–љ–Є–µ –љ–∞–Ї—А–µ—Б—В –ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л —А–∞–≤–љ—Л 90¬∞, —В–Њ —Н—В–Є –і–≤–µ –њ—А—П–Љ—Л–µ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л.
2) –Т –ї—О–±–Њ–є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї –Љ–Њ–ґ–љ–Њ –≤–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М.
3) –¶–µ–љ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —П–≤–ї—П–µ—В—Б—П —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б–µ—А–µ–і–Є–љ–љ—Л—Е –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–Њ–≤ –Ї —Б—В–Њ—А–Њ–љ–∞–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
 –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ –і–Њ –Њ–і–љ–Њ–є –Є–Ј –µ–≥–Њ —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–Њ 17, –∞ –Њ–і–љ–∞ –Є–Ј –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 68. –Э–∞–є–і–Є—В–µ —Г–≥–ї—Л —А–Њ–Љ–±–∞.
–†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ –і–Њ –Њ–і–љ–Њ–є –Є–Ј –µ–≥–Њ —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–Њ 17, –∞ –Њ–і–љ–∞ –Є–Ј –і–Є–∞–≥–Њ–љ–∞–ї–µ–є —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 68. –Э–∞–є–і–Є—В–µ —Г–≥–ї—Л —А–Њ–Љ–±–∞.
–•–Њ–Ј—П–Є–љ —Г—З–∞—Б—В–Ї–∞ –њ–ї–∞–љ–Є—А—Г–µ—В —Г—Б—В—А–Њ–Є—В—М –≤ –ґ–Є–ї–Њ–Љ –і–Њ–Љ–µ –Ј–Є–Љ–љ–µ–µ –Њ—В–Њ–њ–ї–µ–љ–Є–µ. –Ю–љ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ—В –і–≤–∞ –≤–∞—А–Є–∞–љ—В–∞: —Н–ї–µ–Ї—В—А–Є—З–µ—Б–Ї–Њ–µ –Є–ї–Є –≥–∞–Ј–Њ–≤–Њ–µ –Њ—В–Њ–њ–ї–µ–љ–Є–µ. –¶–µ–љ—Л –љ–∞ –Њ–±–Њ—А—Г–і–Њ–≤–∞–љ–Є–µ –Є —Б—В–Њ–Є–Љ–Њ—Б—В—М –µ–≥–Њ —Г—Б—В–∞–љ–Њ–≤–Ї–Є, –і–∞–љ–љ—Л–µ –Њ —А–∞—Б—Е–Њ–і–µ –≥–∞–Ј–∞, —Н–ї–µ–Ї—В—А–Њ—Н–љ–µ—А–≥–Є–Є –Є –Є—Е —Б—В–Њ–Є–Љ–Њ—Б—В–Є –і–∞–љ—Л –≤ —В–∞–±–ї–Є—Ж–µ.
| –Э–∞–≥—А–µ–≤–∞—В–µ–ї—М (–Ї–Њ—В—С–ї) | –Я—А–Њ—З–µ–µ –Њ–±–Њ—А—Г–і–Њ–≤–∞–љ–Є–µ –Є –Љ–Њ–љ—В–∞–ґ | –°—А–µ–і–љ. —А–∞—Б—Е–Њ–і –≥–∞–Ј–∞/ —Б—А–µ–і–љ. –њ–Њ—В—А–µ–±–ї. –Љ–Њ—Й–љ–Њ—Б—В—М | –°—В–Њ–Є–Љ–Њ—Б—В—М –≥–∞–Ј–∞/—Н–ї–µ–Ї—В—А–Њ¬≠—Н–љ–µ—А–≥–Є–Є | |
| –У–∞–Ј–Њ–≤–Њ–µ –Њ—В–Њ–њ–ї–µ–љ–Є–µ | 24 000 —А—Г–±. | 18 280 —А—Г–±. | 1,2 –Ї—Г–±. –Љ/—З | 5,6 —А—Г–±./–Ї—Г–±. –Љ |
| –≠–ї–µ–Ї—В—А. –Њ—В–Њ–њ–ї–µ–љ–Є–µ | 20 000 —А—Г–±. | 15 000 —А—Г–±. | 5,6 –Ї–Т—В | 3,8 —А—Г–±./(–Ї–Т—В*—З) |
–Ю–±–і—Г–Љ–∞–≤ –Њ–±–∞ –≤–∞—А–Є–∞–љ—В–∞, —Е–Њ–Ј—П–Є–љ —А–µ—И–Є–ї —Г—Б—В–∞–љ–Њ–≤–Є—В—М –≥–∞–Ј–Њ–≤–Њ–µ –Њ–±–Њ—А—Г–і–Њ–≤–∞–љ–Є–µ. –І–µ—А–µ–Ј —Б–Ї–Њ–ї—М–Ї–Њ —З–∞—Б–Њ–≤ –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–є —А–∞–±–Њ—В—Л –Њ—В–Њ–њ–ї–µ–љ–Є—П —Н–Ї–Њ–љ–Њ–Љ–Є—П –Њ—В –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П –≥–∞–Ј–∞ –≤–Љ–µ—Б—В–Њ —Н–ї–µ–Ї—В—А–Є—З–µ—Б—В–≤–∞ –Ї–Њ–Љ–њ–µ–љ—Б–Є—А—Г–µ—В —А–∞–Ј–љ–Њ—Б—В—М –≤ —Б—В–Њ–Є–Љ–Њ—Б—В–Є —Г—Б—В—А–Њ–є—Б—В–≤–∞ –≥–∞–Ј–Њ–≤–Њ–≥–Њ –Є —Н–ї–µ–Ї—В—А–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ—В–Њ–њ–ї–µ–љ–Є—П?
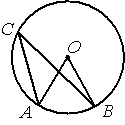 –Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /AOB=84¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ ACB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /AOB=84¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ ACB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
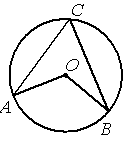 –Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /ACB=65¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ AOB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ґ–Њ—З–Ї–∞ –Ю вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, /ACB=65¬∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ AOB (–≤ –≥—А–∞–і—Г—Б–∞—Е).
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2016-12-09 15:52:33) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ь–∞—А–≥–∞—А–Є—В–∞, –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б –Ї—А–∞—Б–љ—Л–Љ–Є —Б—В–Њ—А–Њ–љ–∞–Љ–Є, AO - —Н—В–Њ –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞, —В–∞–Ї –Ї–∞–Ї –ї–µ–ґ–Є—В –љ–∞–њ—А–Њ—В–Є–≤ –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞.
(2016-12-09 15:35:08) –Ь–∞—А–≥–∞—А–Є—В–∞: –њ—А–Њ—Б—В–Є—В–µ, –Ј–∞–±—Л–ї–∞ —Б–Њ–Њ–±—Й–Є—В—М —Б–≤–Њ—С –Є–Љ—П
(2016-12-09 15:33:20) : –Я–Њ—Г—З–Є–ї–Њ—Б—М –Ї–∞–Ї–Њ–µ-—В–Њ –љ–µ–і–Њ—А–∞–Ј—Г–Љ–µ–љ–Є–µ. –ѓ –љ–∞–њ–Є—Б–∞–ї–∞: –њ–Њ—З–µ–Љ—Г –≤ –≤–∞—А–Є–∞–љ—В–µ 1 AO^2 = 8^2 + 6^2 –≤–µ–і—М AO -–Ї–∞—В–µ—В, –∞ –љ–µ –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞? –Р –≤ –Њ—В–≤–µ—В –Љ–љ–µ –њ—А–Є—И–ї–Њ —Б–Њ–Њ–±—Й–µ–љ–Є–µ, —З—В–Њ –Љ–Њ–є –Ї–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є–є –љ–µ –Њ—В–њ—А–∞–≤–ї–µ–љ, –њ–Њ—В–Њ–Љ—Г —З—В–Њ –Њ–љ —Б–Њ–і–µ—А–ґ–Є—В –љ–µ–љ–Њ—А–Љ–∞—В–Є–≤–љ—Г—О –ї–µ–Ї—Б–Є–Ї—Г.
(2016-12-09 00:00:00) –Ь–∞—А–≥–∞—А–Є—В–∞: –Я–Њ—З–µ–Љ—Г AO2=82+62? –Т–µ–і—М AO - –Ї–∞—В–µ—В, –∞ –љ–µ –≥–Є–њ–Њ—В–µ–љ—Г–Ј–∞.
(2014-12-25 20:57:11) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ц–∞–љ–љ–∞, –љ–µ –≤–Њ –≤—Б–µ—Е –њ–Њ–і–Њ–±–љ—Л—Е –Ј–∞–і–∞—З–∞—Е –њ–Њ–ї—Г—З–∞–µ—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї. –Ъ —В–Њ–Љ—Г –ґ–µ, "–і–Њ—А–Є—Б–Њ–≤–∞—В—М –і–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞" - —Н—В–Њ –љ–µ —В–Њ—З–љ–Њ–µ —А–µ—И–µ–љ–Є–µ, –Љ–Њ–ґ–љ–Њ –Њ—И–Є–±–Є—В—М—Б—П. –Р —А–µ—И–µ–љ–Є–µ –љ–µ —В–∞–Ї–Њ–µ —Г–ґ –Є —Б–ї–Њ–ґ–љ–Њ–µ (–і–ї–Є–љ–љ–Њ–µ - –і–∞, –љ–Њ –љ–µ —Б–ї–Њ–ґ–љ–Њ–µ), 3 —А–∞–Ј–∞ –њ—А–Є–Љ–µ–љ—П–µ—В—Б—П —В–µ–Њ—А–µ–Љ–∞ –Я–Є—Д–∞–≥–Њ—А–∞ –Є –Њ–і–Є–љ —А–∞–Ј —В–µ–Њ—А–µ–Љ–∞ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤.
(2014-12-25 20:42:09) –ґ–∞–љ–љ–∞: –Ј–і–µ—Б—М –ї–µ–≥–Ї–Њ –і–Њ—А–Є—Б–Њ–≤–∞—В—М –і–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –Њ–і–Є–љ –Ї–∞—В–µ—В –≤ 2 —А–∞–Ј–∞ –±–Њ–ї—М—И–µ –і—А—Г–≥–Њ–≥–Њ
(2014-12-25 20:37:50) –ґ–∞–љ–љ–∞: —Н—В–Є —А–µ—И–µ–љ–Є—П —Б–ї–Њ–ґ–љ—Л–µ –і–ї—П 9 –Ї–ї–∞—Б—Б–∞
(2014-05-17 10:26:18) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Х–≤–≥–µ–љ–Є–є, –Є–љ—В–µ—А–µ—Б–љ–∞—П –Љ—Л—Б–ї—М, –Љ—Л –њ—А–Њ—А–µ—И–∞–µ–Љ –Є –≤—Л–ї–Њ–ґ–Є–Љ –Т–∞—И –≤–∞—А–Є–∞–љ—В —А–µ—И–µ–љ–Є—П. –°–њ–∞—Б–Є–±–Њ –Ј–∞ –њ–Њ–і—Б–Ї–∞–Ј–Ї—Г.
(2014-05-17 09:01:43) –Х–≤–≥–µ–љ–Є–є : –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –Ї–Њ—Б–Є–љ—Г—Б —Г–≥–ї–∞ –њ–Њ —В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤, –њ–Њ—В–Њ–Љ –љ–∞–є—В–Є —Б–Є–љ—Г—Б –Є —В–∞–љ–≥–µ–љ—Б
(2014-05-12 09:19:35) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: evg-bakin@yandex.ru, –Ї —Б–Њ–ґ–∞–ї–µ–љ–Є—О, –љ–µ –≤—Б–µ–≥–і–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –њ–Њ–ї—Г—З–∞–µ—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–Љ. –Э–∞–њ—А–Є–Љ–µ—А, –≤ –Ј–∞–і–∞—З–∞—Е вДЦ405 –Є вДЦ472 —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Њ—З–µ–≤–Є–і–љ–Њ –љ–µ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є.
(2014-05-12 08:22:12) evg-bakin@yandex.ru: –љ—Г–ґ–љ–Њ –њ–Њ—Б—В—А–Њ–Є—В—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї, –љ–∞–є—В–Є –і–ї–Є–љ—Л —Б—В–Њ—А–Њ–љ, –њ–Њ—Б–Љ–Њ—В—А–µ—В—М –±—Г–і–µ—В –ї–Є —Н—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–Љ. –Р –Њ–љ –і–Њ–ї–ґ–µ–љ –±—Л—В—М!
(2014-05-11 19:29:49) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Э–∞–і—П, –і–∞, —П –≤ –Ї—Г—А—Б–µ, –љ–Њ –і—А—Г–≥–Њ–≥–Њ, —Б—В—А–Њ–≥–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–µ—И–µ–љ–Є—П –љ–∞–є–і–µ–љ–Њ –љ–µ –±—Л–ї–Њ. –£—З–Є—В–µ–ї—М –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –Њ–і–љ–Њ–є —И–Ї–Њ–ї—Л –њ—А–µ–і–ї–Њ–ґ–Є–ї –њ—А–Є–Ї–ї–∞–і—Л–≤–∞—В—М —Г–≥–Њ–ї—М–љ–Є–Ї –Є –і–Њ—А–Є—Б–Њ–≤—Л–≤–∞—В—М –і–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –љ–Њ —Н—В–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ–Њ —В–Њ–ї—М–Ї–Њ, –µ—Б–ї–Є —А–∞–Ј—А–µ—И–∞—В –њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П —Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–µ. –Ш –њ–ї—О—Б –Љ–Њ–ґ–µ—В –њ–Њ–ї—Г—З–Є—В—М—Б—П –љ–µ —В–Њ—З–љ–Њ. –Я–Њ—Н—В–Њ–Љ—Г, –і—Г–Љ–∞—О, —З—В–Њ –ї—Г—З—И–µ –Ј–∞–њ–Њ–Љ–љ–Є—В—М —Н—В—Г —Д–Њ—А–Љ—Г–ї—Г.
(2014-05-11 19:06:56) –Э–∞–і—П: –Т 9 –Ї–ї–∞—Б—Б–µ —Д–Њ—А–Љ—Г–ї–∞ —В–∞–љ–≥–µ–љ—Б–∞ —А–∞–Ј–љ–Њ—Б—В–Є –і–≤—Г—Е —Г–≥–ї–Њ–≤ –љ–µ –Є–Ј—Г—З–∞–µ—В—Б—П