
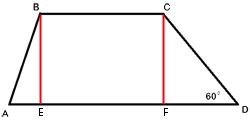
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
 Проведем
высоты BE и CF как показано на рисунке.
Проведем
высоты BE и CF как показано на рисунке.
Рассмотрим треугольник CDF. Он
прямоугольный, т.к. CF-высота.
По
теореме о сумме углов треугольника /FCD=180°-90°-60°=30°.
По
определению синуса sin/FCD=DF/CD=sin30°=1/2
Т.е. DF=CD/2, CD, в свою очередь, по условию задачи равно AD/2, получаем, что DF=AD/4.
BC=AD/2 (по условию задачи)
EF=BC=AD/2 (т.к. BCFE - прямоугольник)
Вычислим AE, AE=AD-DF-EF=AD-AD/4-AD/2=AD/4, т.е. мы получили, что AE=FD
Рассмотрим треугольники ABC и DCF:
BE=CF (т.к. BCFE - прямоугольник)
AE=FD (только что получили)
/AEB=90°=/DFC, тогда по
первому признаку равенства, треугольники ABC и DCF равны.
Следовательно, AB=CD, т.е. наша
трапеция равнобедренная.
AB=CD=2 (по условию задачи), AD=2*CD=2*BC=4 (тоже по условию), BC=CD=2
FD=AD/4=1
По
теореме Пифагора CD2=CF2+FD2
22=CF2+12
CF2=3, CF=√
SABCD=((BC+AD)/2)*CF=((2+4)/2)*√
SABCD=3√
Ответ: SABCD=3√
Поделитесь решением
Присоединяйтесь к нам...
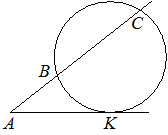 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Комментарии:
(2015-05-09 14:32:31) Администратор: Влад, спасибо за найденную опечатку, исправлено.
(2015-05-07 21:27:18) Влад: Есть ошибка в решении, вроде бы. Написано: "уголAEF = 90 = углуDFC" А должно быть, вроде, уголAEB = 90 = углуDFC