
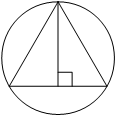
 Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
По
третьему свойству
равностороннего треугольника:
R=a√
6=a√
18=a√
a=18/√
По второму свойству:
h=a*√
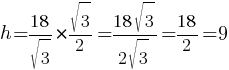
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
 Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB=26.
 В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
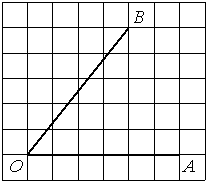 Найдите тангенс угла AOB, изображённого
на рисунке.
Найдите тангенс угла AOB, изображённого
на рисунке.
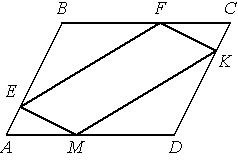 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
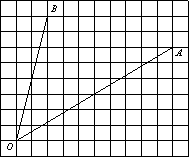 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Комментарии: