
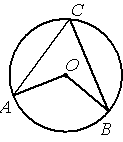
 Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=128°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 128°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 128/2=64.
Ответ: /ACB=64°.
Поделитесь решением
Присоединяйтесь к нам...
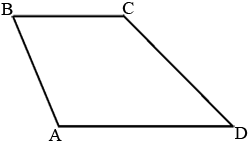 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
 В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 164. Найдите стороны треугольника ABC.
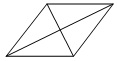 Найдите площадь ромба, если его диагонали равны 39 и 2.
Найдите площадь ромба, если его диагонали равны 39 и 2.
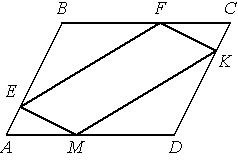 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
 Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Комментарии: