Автор: страдалец
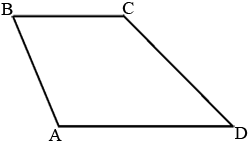
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Проведем
высоты, как показано на рисунке.
Эти
высоты, естественно, равны друг другу.
∠DCE=∠BCD-90° (так как CE-
высота)
∠DCE=150°-90°=60°
cos∠DCE=CE/CD (по
определению косинуса).
cos60°=CE/32
CE=32cos60° (по
таблице cos60°=1/2=0,5).
CE=32*0,5=16
CE=AF=16 (как уже было сказано ранее).
sin∠ABC=AF/AB (по
определению синуса).
sin45°=16/AB
AB=16/sin45° (по
таблице sin45°=√
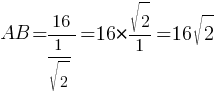
Ответ: 16√
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите величину угла BOC. Ответ дайте в градусах.
Найдите площадь треугольника, изображённого на рисунке.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
Хочу получать новые решения
Ни какого спама
Комментарии: