Найдите площадь ромба, если его диагонали равны 39 и 2.
Площадь
ромба можно найти по формуле:
S=ab/2, где a и b - диагонали ромба.
Тогда:
S=ab/2=39*2/2=39
Ответ: 39
Поделитесь решением
Присоединяйтесь к нам...
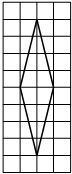На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=11, CK=20.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: