
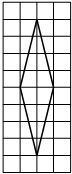
 На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите площадь этого ромба.
 Проведем диагонали ромба.
Проведем диагонали ромба.
Диагонали делят ромб на 4 треугольника.
Эти треугольники прямоугольные, так как диагонали пересекаются под прямым углом (по
свойству ромба).
Учитывая второе свойство ромба, получается что у треугольников равны соответственные стороны.
Тогда, эти треугольники равны, по
третьему признаку равенства.
Площадь прямоугольного треугольника:
S=ab/2, где а и b - катеты треугольника.
S=1*4/2=2
Sромб=4S=4*2=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
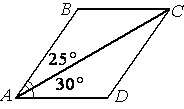 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Диагонали ромба перпендикулярны.
3) Площадь треугольника меньше произведения двух его сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
 Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=24, MN=18. Найдите AM.
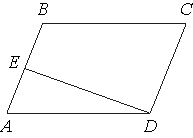 Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Комментарии: