
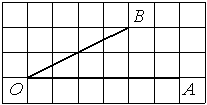
 Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
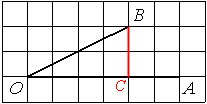 В данной задаче надо просто дорисовать угол до прямоугольного треугольника. При этом длину сторон угла можно выбрать по своему усмотрению, поэтому выберем так, чтобы стороны составляли целое число клеточек.
В данной задаче надо просто дорисовать угол до прямоугольного треугольника. При этом длину сторон угла можно выбрать по своему усмотрению, поэтому выберем так, чтобы стороны составляли целое число клеточек.
Тогда по определению тангенса:
tg∠BOC=BC/OC=2/4=0,5
Ответ: 0,5
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
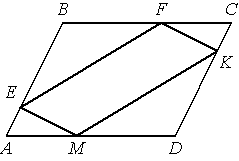 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
 Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K,
длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K,
длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
Комментарии: