
 Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Сторона ромба равна 38, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
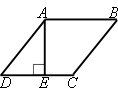 150° - это тупой угол, т.е. это ∠DAB и ∠BCD (эти углы равны по
свойству параллелограмма и ромба).
150° - это тупой угол, т.е. это ∠DAB и ∠BCD (эти углы равны по
свойству параллелограмма и ромба).
AB||CD (по определению параллелограмма и ромба).
Тогда:
∠DEA=∠BAE=90° (это
накрест лежащие углы).
Следовательно:
∠DAE=∠DAB-∠EAB=150°-90°=60°
Треугольник DAE - прямоугольный, тогда, по определению косинуса:
cos∠EAB=AE/AD
cos60°=AE/38
1/2=AE/38 (по таблице косинусов)
AE=38/2=19 - это и есть
высота.
Ответ: 19
Поделитесь решением
Присоединяйтесь к нам...
 Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Углы B и C треугольника ABC равны соответственно 65° и 85°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 14.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
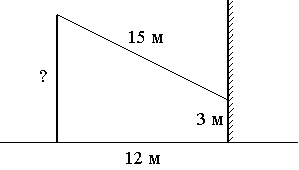 От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
 Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1.
 В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
Комментарии:
(2023-12-19 12:31:20) Fdggf: Fezzxc!???