
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ593 –Η–Ζ 1087 |
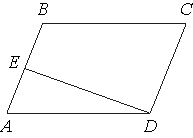 –ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD ―Ä–Α–≤–Ϋ–Α 6. –Δ–Ψ―΅–Κ–Α E βÄ™ ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η EBCD.
–ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD ―Ä–Α–≤–Ϋ–Α 6. –Δ–Ψ―΅–Κ–Α E βÄ™ ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η EBCD.
–£–Α―Ä–Η–Α–Ϋ―² ⳕ1
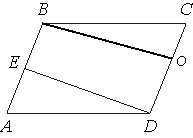 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –≤―΄―¹–Ψ―²―É
–Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α BO, –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β. –ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―é ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Ϋ–Α –≤―΄―¹–Ψ―²―É
–Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –≤―΄―¹–Ψ―²―É
–Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α BO, –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β. –ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―Ä–Α–≤–Ϋ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―é ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Ϋ–Α –≤―΄―¹–Ψ―²―É
–Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α.
S–Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α=CD*h=6
–ê –Ω–Μ–Ψ―â–Α–¥―¨
―²―Ä–Α–Ω–Β―Ü–Η–Η ―Ä–Α–≤–Ϋ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η―é –Ω–Ψ–Μ―É―¹―É–Φ–Φ―΄ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Ι –Ϋ–Α –≤―΄―¹–Ψ―²―É.
S―²―Ä–Α–Ω–Β―Ü–Η–Η=h*(EB+CD)/2.
EB=AB/2 (–Ω–Ψ ―É―¹–Μ–Ψ–≤–Η―é –Ζ–Α–¥–Α―΅–Η).
AB=CD (–Ω–Ψ
―¹–≤–Ψ–Ι―¹―²–≤―É –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α).
–Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ EB=CD/2.
–Δ–Ψ–≥–¥–Α S―²―Ä–Α–Ω–Β―Ü–Η–Η=h*(CD/2+CD)/2 = h*(3*CD/2)/2 = h*3*CD/4=h*CD*3/4 = S–Ω–Α―Ä–Α–Μ-–Φ–Α*3/4=6*3/4=4,5.
–û―²–≤–Β―²: 4,5
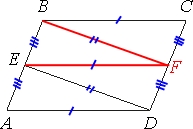 –ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Κ–Η –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.
–ü―Ä–Ψ–≤–Β–¥–Β–Φ –Ψ―²―Ä–Β–Ζ–Κ–Η –Κ–Α–Κ –Ω–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ –Ϋ–Α ―Ä–Η―¹―É–Ϋ–Κ–Β.–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ, –Κ–Ψ―²–Ψ―Ä―΄–Ι –Ψ–±―Ä–Α–Ζ―É―é―² –Φ–Η–Ϋ―É―²–Ϋ–Α―è –Η ―΅–Α―¹–Ψ–≤–Α―è ―¹―²―Ä–Β–Μ–Κ–Η ―΅–Α―¹–Ψ–≤ –≤ 11:00. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ, –Κ–Ψ―²–Ψ―Ä―΄–Ι –Ψ–±―Ä–Α–Ζ―É―é―² –Φ–Η–Ϋ―É―²–Ϋ–Α―è –Η ―΅–Α―¹–Ψ–≤–Α―è ―¹―²―Ä–Β–Μ–Κ–Η ―΅–Α―¹–Ψ–≤ –≤ 11:00. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC. –Δ–Ψ―΅–Κ–Α O ―è–≤–Μ―è–Β―²―¹―è ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η―è –Ψ―² ―²–Ψ―΅–Κ–Η O –¥–Ψ ―²–Ψ―΅–Κ–Η A –Η –Ω―Ä―è–Φ―΄―Ö AD –Η AC ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ ―Ä–Α–≤–Ϋ―΄ 25, 13 –Η 7. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Α –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC. –Δ–Ψ―΅–Κ–Α O ―è–≤–Μ―è–Β―²―¹―è ―Ü–Β–Ϋ―²―Ä–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, –≤–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC. –†–Α―¹―¹―²–Ψ―è–Ϋ–Η―è –Ψ―² ―²–Ψ―΅–Κ–Η O –¥–Ψ ―²–Ψ―΅–Κ–Η A –Η –Ω―Ä―è–Φ―΄―Ö AD –Η AC ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ ―Ä–Α–≤–Ϋ―΄ 25, 13 –Η 7. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD.
 –ù–Α–Ι–¥–Η―²–Β –±–Ψ–Μ―¨―à–Η–Ι ―É–≥–Ψ–Μ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ AD –Η –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι AB ―É–≥–Μ―΄, ―Ä–Α–≤–Ϋ―΄–Β 46¬Α –Η 35¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α–Ι–¥–Η―²–Β –±–Ψ–Μ―¨―à–Η–Ι ―É–≥–Ψ–Μ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ AD –Η –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι AB ―É–≥–Μ―΄, ―Ä–Α–≤–Ϋ―΄–Β 46¬Α –Η 35¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –ù–Α–Ι–¥–Η―²–Β –±–Ψ–Μ―¨―à–Η–Ι ―É–≥–Ψ–Μ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ AD –Η –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι AB ―É–≥–Μ―΄, ―Ä–Α–≤–Ϋ―΄–Β 46¬Α –Η 35¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–ù–Α–Ι–¥–Η―²–Β –±–Ψ–Μ―¨―à–Η–Ι ―É–≥–Ψ–Μ ―Ä–Α–≤–Ϋ–Ψ–±–Β–¥―Ä–Β–Ϋ–Ϋ–Ψ–Ι ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC –Ψ–±―Ä–Α–Ζ―É–Β―² ―¹ –Ψ―¹–Ϋ–Ψ–≤–Α–Ϋ–Η–Β–Φ AD –Η –±–Ψ–Κ–Ψ–≤–Ψ–Ι ―¹―²–Ψ―Ä–Ψ–Ϋ–Ψ–Ι AB ―É–≥–Μ―΄, ―Ä–Α–≤–Ϋ―΄–Β 46¬Α –Η 35¬Α ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
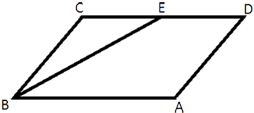 –ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α
ABCD ―Ä–Α–≤–Ϋ–Α 30. –Δ–Ψ―΅–Κ–Α E βÄ™ ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ CD. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABED.
–ü–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α
ABCD ―Ä–Α–≤–Ϋ–Α 30. –Δ–Ψ―΅–Κ–Α E βÄ™ ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ CD. –ù–Α–Ι–¥–Η―²–Β –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η ABED.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2017-05-28 22:46:35) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: Alissa, –Ψ―²–Μ–Η―΅–Ϋ–Ψ–Β ―Ä–Β―à–Β–Ϋ–Η–Β, ―¹–Ω–Α―¹–Η–±–Ψ!
(2017-05-20 12:39:40) Alissa: –€–Ψ–Ε–Ϋ–Ψ –¥–Ψ–Κ–Α–Ζ–Α―²―¨, ―΅―²–Ψ –Ω–Μ–Ψ―â–Α–¥―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ―¹–Ψ―¹―²–Ψ–Η―² –Η–Ζ 4―Ö ―Ä–Α–≤–Ϋ–Ψ–≤–Β–Μ–Η–Κ–Η―Ö ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Ψ–≤. –ü–Ψ―ç―²–Ψ–Φ―É, –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ADE ―¹–Ψ―¹―²–Α–≤–Μ―è–Β―² 1/4 –Ω–Μ–Ψ―â–Α–¥–Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. –Δ–Ψ–≥–¥–Α –Ω–Μ–Ψ―â–Α–¥―¨ ―²―Ä–Α–Ω–Β―Ü–Η–Η –ï–£–ΓD ―¹–Ψ―¹―²–Α–≤–Μ―è–Β―² 3/4 –Ω–Μ–Ψ―â–Α–¥–Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α .S=3/4*6=4,5 .–û―²–≤–Β―²:4,5
(2017-03-04 11:23:10) –¦―è–Μ―è: –Γ–Ω–Α―¹–Η–±–Ψ,–≤―¹―ë –Ψ―΅–Β–Ϋ―¨ –Ω–Ψ–Ϋ―è―²–Ϋ–Ψ –Η –Ω―Ä–Ψ―¹―²–Ψ!