
 Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 35° соответственно. Ответ дайте в градусах.
По свойству
равнобедренной трапеции - углы при основании равны.
Тогда ∠ADC=46°+35°=81°.
Сумма углов четырехугольника равна 360°, тогда получаем, что:
360°=81°+81°+∠DCB+∠CBA,
∠DCB+∠CBA=360°-81°-81°=198°, а учитывая, что ∠DCB=∠CBA (по тому
свойству равнобедренной трапеции), получаем ∠DCB=∠CBA=198°/2=99°, эти углы и есть бОльшие в трапеции
Ответ: 99
Поделитесь решением
Присоединяйтесь к нам...
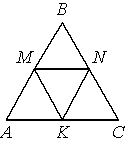 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
 Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
 В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
 Площадь прямоугольного треугольника равна 18√
Площадь прямоугольного треугольника равна 18√
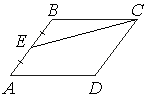 Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
Комментарии: