Автор: страдалец
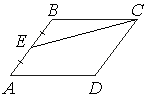
Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
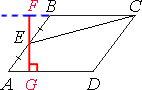Проведем перпендикулярный отрезок от одной стороны
параллелограмма к другой через точку Е, как показано на рисунке.
Обозначим концы отрезка как F и G.
FG - высота параллелограмма, так как перпендикулярен двум сторонам (мы сами так его провели).
Площадь параллелограмма:
SABCD=FG*AD=FG*BC
Рассмотрим треугольники AEG и BEF:
AE=EB (по условию задачи).
∠AEG=∠BEF (они вертикальные).
∠GAE=∠FBE (они накрест-лежащие).
Тогда, по второму признаку равенства треугольников, данные треугольники равны.
Это означает, что EF=EG=FG/2
EF - высота треугольника CBE.
Воспользуемся формулой
площади треугольника через высоту и основание:
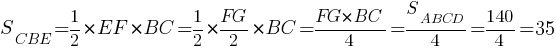
Ответ: 35
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Найдите площадь квадрата, описанного около окружности радиуса 32.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Высота равностороннего треугольника равна 96√
Хочу получать новые решения
Ни какого спама
Комментарии: