К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
Проведем отрезок ОВ.
Отрезок OB - это радиус окружности и этот отрезок перпендикулярен AB (по
свойству
касательной).
Следовательно, треугольник AOB -
прямоугольный, тогда, по
теореме Пифагора:
AO2=AB2+OB2
852=402+OB2
7225=1600+OB2
OB2=5625
OB=75=R
Ответ: 75
Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Треугольника со сторонами 1, 2, 4 не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
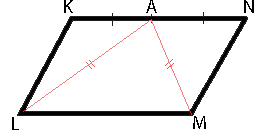В параллелограмме KLMN точка A — середина стороны KN. Известно, что AL=AM. Докажите, что данный параллелограмм — прямоугольник.
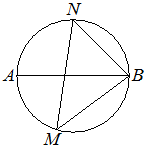На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
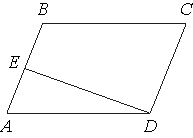Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-05-05 11:40:38) Администратор: Коля, Вы имеете ввиду написать само слово \"Дано\"?
(2019-05-05 10:35:58) коля : напишите пожалуста дано спасибо