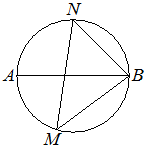
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
∠NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 41°*2=82°.
Тогда дуга NB равна 180°-82°=98°
∠NMB - тоже является
вписанным в окружность и опирается на дугу NB, следовательно он равен 98°/2=49°
Ответ: 49
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=17. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
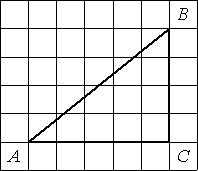Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
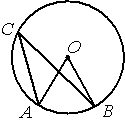Точка О – центр окружности, /ACB=32° (см. рисунок). Найдите величину угла AOB (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: