Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Площадь
трапеции вычисляется по формуле 
, где a и b - основания трапеции, а h - высота трапеции. Обозначим углы трапеции A, B, C и D. И проведем высоту из угла B к основанию AD, как паказано на рисунке.
Получившийся треугольник ABP -
прямоугольный c катетами BP и AP. Заметим, что BP - это катет притиволежащий углу в 30°, следовательно он равен половине гипотенузы (
по свойству прямоугольного треугольника), h=3/2=1,5. Используя формулу площади трапеции получаем S=(2+6)*1,5/2. Вычисляем S=6.
Ответ: S=6.
Поделитесь решением
Присоединяйтесь к нам...
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Найдите площадь треугольника, изображённого на рисунке.
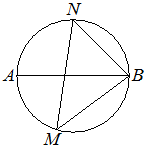На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-02-06 21:50:52) Дарья: Спасибо огромное автору и сайту за проделанную работу.Это очень помогает и выручает в той ситуации,когда не можешь решить то или иное задание.Спасибо!