
Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Рассмотрим каждое утверждение:
1) "Все углы ромба равны". Ромб, у которого все углы равны - это уже
квадрат. Не каждый
ромб является
квадратом, следовательно данное утверждение неверно.
2) "Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны" - это утверждение неверно. Можно привести простой пример:
квадрат и
ромб с равными сторонами - стороны равны, а четырехугольники не равны.
3) "Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности" - это утверждение верно по
второму свойству касательной.
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
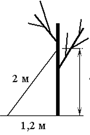 Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
 В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
 На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=36, BC=42 и CD=24.
На стороне AB треугольника ABC взята такая точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=36, BC=42 и CD=24.
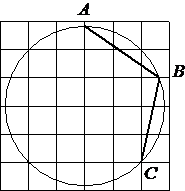 Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
Комментарии: