
 ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
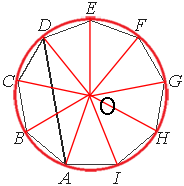 Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠DOE) равен 360°/9=40°
Тогда ∠AOC, который опирается на дугу ABC равен:
∠AOC=40°*2=80°
∠AOC является
центральным, следовательно градусная мера дуги ABC тоже равна 80°
∠ADC тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠ADC=80°/2=40° (по
теореме о вписанном угле)
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
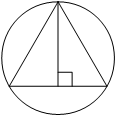 Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 6. Найдите высоту этого треугольника.
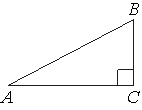 В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
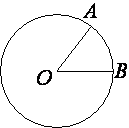 На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
 Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Комментарии: