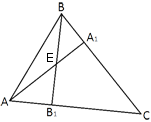Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
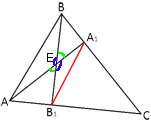Проведем отрезок A1B1 и рассмотрим треугольники EB1A и EA1B.
∠A1EB=∠B1EA (так как они
вертикальные).
∠EB1A=∠EA1B=90° (так как BB1 и AA1 -
высоты).
По
первому признаку подобия треугольников, рассматриваемые треугольники
подобны.
Следовательно:
EB1/EA1=EA/EB
Рассмотрим треугольники EA1B1 и EAB
∠BEA=∠B1EA1 (так как они
вертикальные).
Как мы выяснили ранее:
EB1/EA1=EA/EB
Умножим левую и правую части равенства на EA1, получим:
EB1=EA1*EA/EB
Разделим левую и правую части на EA, получаем:
EB1/EA=EA1/EB
Получается, что по
второму признаку подобия треугольников, треугольники EA1B1 и EAB
подобны.
Следовательно, по
определению, углы AA1B1 и ABB1 равны.
Поделитесь решением
Присоединяйтесь к нам...
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Стороны AC, AB, BC треугольника ABC равны 3√
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
Лестница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-10 22:22:34) Администратор: Дмитрий, если не сложно, то пришлите, пожалуйста, Ваш вариант решения на admin@otvet-gotov.ru
(2017-05-08 09:36:21) Дмитрий: С помощью описанной окружности решение короче и легче