
 Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
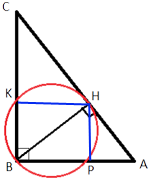 Проведем отрезки KH и HP.
Проведем отрезки KH и HP.
Треугольники BKH и BPH являются
вписанными в данную окружность. А т.к. центр этой окружности располагается на середине их стороны BH, то это означает, что эти треугольники прямоугольные с гипотенузой BH (по
свойству описанной окружности).
Следовательно, ∠HKB и ∠HPB - прямые.
Рассмотрим четырехугольник BKHP, сумма углов любого четырехугольника равна 360°, следовательно ∠HKB+∠KBP+∠HPB+∠PHK=360°
90°+90°+90°+∠PHK=360°
∠PHK=90°
То есть получается, что четырехугольник BKHP является
прямоугольником. Диагонали этого прямоугольника BH и PK.
PK=BH=13 (по свойству
прямоугольника)
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?
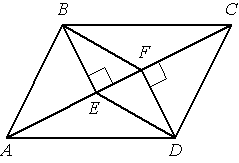 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
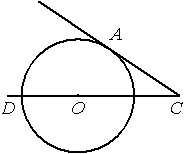 Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
130°.
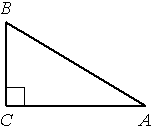 В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
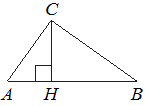 На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
Комментарии: