ОГЭ, Математика.
Геометрия: Задача №E5A864
| Задача №1036 из 1087
Условие задачи: | |
 Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Решение задачи:
Вариант №1
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=∠A+66°+84°
∠A=180°-66°-84°=30°
По
теореме синусов:
2R=BC/sin∠A
2R=BC/sin30°=BC/(1/2)=2BC
R=BC=15
Ответ: 15
Вариант №2 (Предложил пользователь Надежда)
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=∠A+66°+84°
∠A=180°-66°-84°=30°
∠A - это
вписанный в окружность угол, следовательно, дуга, на которую он опирается, имеет вдвое большую градусную меру 2*30°=60° (по
теореме о вписанном угле).
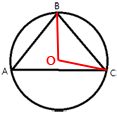
Проведем два отрезка из центра к точкам B и C, как показано на рисунке.
∠BOC - это
центральный угол, следовательно, равен градусной мере дуги, на которую он опирается.
Как мы выяснили ранее, градусная мера этой дуги равна 60°. Т.е. ∠BOC=60°
Рассмотрим треугольник OBC.
OB=OC=R, следовательно, данный треугольник
равнобедренный.
Значит:
∠OBC=∠OCB=x (по
свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠OBC+∠OCB+∠BOC
180°=x+x+60°
180°-60°=2x
x=60°
Т.е. все углы этого треугольника равны 60°.
Следовательно, данный треугольник
равносторонний (по
свойству равностороннего треугольника).
Тогда:
OB=OC=BC=15 (по
определению).
Ответ: 15
Вы можете поблагодарить автора, написать свои претензии или предложения на
странице 'Про нас'
Другие задачи из этого раздела
 Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
 Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
 Высота равностороннего треугольника равна 96√3. Найдите его периметр.
Высота равностороннего треугольника равна 96√3. Найдите его периметр.
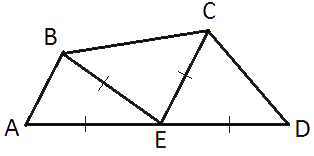 Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
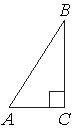 В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.

 Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15. Проведем два отрезка из центра к точкам B и C, как показано на рисунке.
Проведем два отрезка из центра к точкам B и C, как показано на рисунке. Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту. Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности. Высота равностороннего треугольника равна 96√
Высота равностороннего треугольника равна 96√ Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°. В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Комментарии: