
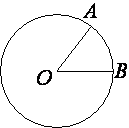
 На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
∠AOB является центральным, поэтому градусная мера дуги, на которую он опирается тоже равна 66°.
Так как градусная мера всей окружности составляет 360°, то градусная мера большей дуги равна:
360°-66°=294°
Теперь систавим пропорцию:
Для 66° - длина дуги 99
Для 294° - длина дуги x
66/294=99/x
x=294*99/66=294*1,5=441
Ответ: 441
Поделитесь решением
Присоединяйтесь к нам...
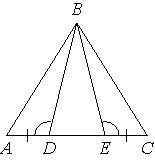 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
 В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
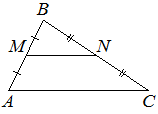 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
 Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
Комментарии: