
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
Рассмотрим треугольник ABF.
По свойству
биссектрисы:
BG/GF=AB/AF=17/15
cosA=AF/AB=15/17 (по
определению косинуса)
Существует тригонометрическая формула:
sin2α+cos2α=1
Тогда:
sin2∠BAF+cos2∠BAF=1
sin2∠BAF+(15/17)2=1
sin2∠BAF=1-225/289
sin2∠BAF=(289-225)/289
sin2∠BAF=64/289
sin∠BAF=8/17
По
теореме синусов:
BC/sin∠BAF=2R
16/(8/17)=16*17/8=34=2R
R=34/2=17
Ответ: R=17
Поделитесь решением
Присоединяйтесь к нам...
 На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
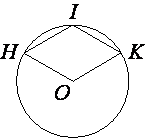 Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OKI. Ответ дайте в градусах.
 Катеты прямоугольного треугольника равны 4√
Катеты прямоугольного треугольника равны 4√
 Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:7, KM=12.
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:7, KM=12.
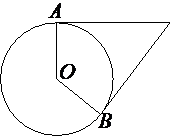 Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Комментарии:
(2014-05-14 20:55:14) Аделя: конечно из 2 части.