Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
Вариант №1 Предложила пользователь Надя.
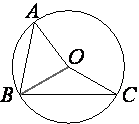Проведем отрезок OB.
Рассмотрим треугольник AOB.
Так как AO=BO (это радиусы окружности), то данный треугольник
равнобедренный.
Следовательно, ∠OAB=∠ABO=8° (по
свойству равнобедренного треугольника)
∠OBC=∠ABC-∠ABO=15°-8°=7°.
Треугольник BOC тоже
равнобедренный, т.к. OB=OC (радиусы окружности).
Следовательно, ∠OBC=∠BCO=7° (по
свойству).
Ответ: 7.
Вариант №2
Продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).
Рассмотрим треугольник ABE. По
теореме о сумме углов треугольника запишем:
180°=∠OAB+∠ABC+∠BEA
180°=8°+15°+∠BEA
∠BEA=180°-8°-15°=157°
Смежный этому углу ∠OEC=180°-∠BEA=180°-157°=23° (запомним это)
Угол ABC является
вписанным углом, следовательно градусная мера дуги, на которую он опирается, вдвое больше (по
теореме о вписанном угле), т.е. градусная мера дуги AC равна 15°*2=30°
Угол АОС является
центральным и, соответственно, равен градусной мере дуги, на которую опирается. А опирается он на дугу AC, следовательно ∠AOC=30°
Смежный этому углу ∠COE=180°-∠AOC=180°-30°=150°
Рассмотрим треугольник OCE.
По
теореме о сумме углов треугольника запишем:
180°=∠OEC+∠COE+∠OCE
Вспомнив то, что запомнили ранее...
180°=23°+150°+∠OCE
∠OCE=180°-23°-150°=7°
∠OCE и есть искомый угол BCO.
Ответ: ∠BCO=7°
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.
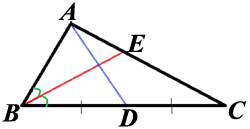В треугольнике ABC биссектриса BE и медиана AD перпендикулярны
и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
Стороны AC, AB, BC треугольника ABC равны 2√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-24 16:29:10) алексей: Большое спасибо разработчикам сайта. Очень помогли.
(2014-11-29 23:16:26) Администратор: Денис, очень неплохое решение. Решений может быть очень много, например доказательств теоремы Пифагора около 600 (если не ошибаюсь).
(2014-11-29 20:55:25) Денис: Я по другому решил. Вот решение, ТОЛЬКО смысл постараюсь передать: 1)в четырехугольнике сумма углов = 360 2)т.к. АВС вписанный угол а АОС центральный опираются на одну и ту жу дугу значит АОС(меньший) =30 градусам. 3) значит угол АОС больший будут равен (360-30)=330 градусам 4)360=(330+8+15+ВСО) 360=345+8+ВСО 15=8+ВСО ВСО=7 градусов Ответ: 7