
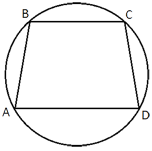 Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Описать окружность можно только около
равнобокой трапеции (по
свойству трапеции).
Получается, что наша
трапеция - равнобокая (или равнобедренная).
Пусть 49° равняется угол BAD.
∠BAD=∠ADC=49° (по
свойству равнобедренной трапеции).
Сумма углов выпуклого n-угольника вычисляется по формуле (n-2)180°, тогда сумма углов трапеции равна (4-2)180°=360°.
360°=∠BAD+∠ADC+∠DCB+∠CBA
360°=49°+49°+∠DCB+∠CBA
∠DCB+∠CBA=262°
∠DCB=∠CBA (по
свойству равнобедренной трапеции).
Тогда ∠DCB=∠CBA=262°/2=131°
Ответ: ∠DCB=∠CBA=131°, ∠BAD=∠ADC=49°
Поделитесь решением
Присоединяйтесь к нам...
 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.
 Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
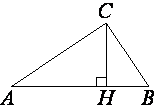 В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника BKP к площади треугольника AMK.
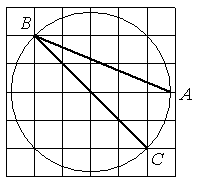 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
Комментарии:
(2015-05-16 19:27:30) Светлана: Пусть угол А равен 39 гр. Углы А и В внутренние односторонние при параллельных BC и АD и секущей AB. Тогда угол B равен 180-39 = 141. Условие вписанного в окружность четырёхугольника: сумма противоположных углов равна 180 градусов. Значит угол С равен 180-39 = 141. Тогда на угол D приходится 39 градусов.
(2015-05-05 12:17:53) Жека: АВТАР ВАЩЕ КРАСАВА