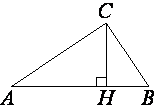
В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
Рассмотрим треугольники ABC и ACH.
∠AHC=∠ACB (т.к. это прямые углы).
∠A - общий.
Следовательно, по
теореме о сумме углов треугольника ∠ACH=∠ABC
Тогда sin∠ACH=sin∠ABC.
Теперь рассмотрим треугольник ACH.
По
теореме Пифагора:
AC2=CH2+AH2
82=(2√
64=4*15+AH2
AH2=64-60
AH2=4
AH=2
sin∠ACH=AH/AC (по
определению)
sin∠ACH=2/8=1/4=0,25
Как было выведено выше:
sin∠ABC=sin∠ACH=0,25
Ответ: sin∠ABC=0,25
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь треугольника, изображённого на рисунке.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
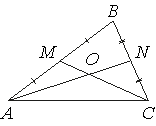Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
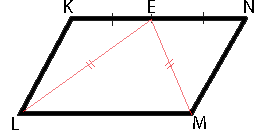В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-05-11 09:37:59) Администратор: Олеся, к сожалению, у меня нет такой информации.
(2016-05-11 09:36:57) Олеся: Ответьте пожалуйста, на экзамене эта задача под каким номером. Из второй части?
(2016-05-11 09:32:39) Олеся: Ответьте пожалуйста, на экзамене эта задача под каким номером. Из второй части?