
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ801 –Є–Ј 1087 |
 –°—В–Њ—А–Њ–љ—Л AC, AB, BC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ—Л 2√
–°—В–Њ—А–Њ–љ—Л AC, AB, BC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ—Л 2√
–Я–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є ∠KAC>90¬∞, —В.–µ. —Н—В–Њ –љ–∞–Є–±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ AKC —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Б—В–Њ—А–Њ–љ–∞ KC, –њ—А–Њ—В–Є–≤–Њ–ї–µ–ґ–∞—Й–∞—П —Н—В–Њ–Љ—Г —Г–≥–ї—Г —В–Њ–ґ–µ –љ–∞–Є–±–Њ–ї—М—И–∞—П (–њ–Њ —В–µ–Њ—А–µ–Љ–µ –Њ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П—Е –Љ–µ–ґ–і—Г —Б—В–Њ—А–Њ–љ–∞–Љ–Є –Є —Г–≥–ї–∞–Љ–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞). –°—В–Њ—А–Њ–љ–∞ AC —А–∞–≤–љ–∞—П 2√
–Я–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї KAC –њ–Њ–і–Њ–±–µ–љ –Є—Б—Е–Њ–і–љ–Њ–Љ—Г —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї—Г ABC. –Р –Ј–љ–∞—З–Є—В —Г–≥–ї—Л —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ —А–∞–≤–љ—Л (–њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–Њ–і–Њ–±–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤). –Я–Њ—Н—В–Њ–Љ—Г –љ–∞–Є–±–Њ–ї—М—И–Є–µ —Г–≥–ї—Л –і–≤—Г—Е —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —А–∞–≤–љ—Л, —В.–µ. ∠KAC=∠ABC. ∠ACK –љ–µ —А–∞–≤–µ–љ ∠ACB ( —В.–Ї. KC –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Г AB –≤ —В–Њ—З–Ї–µ, –Њ—В–ї–Є—З–љ–Њ–є –Њ—В B), –њ–Њ—Н—В–Њ–Љ—Г ∠ACK = ∠BAC. –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, ∠AKC=∠ACB => cos(∠AKC)=cos(∠ACB).
–Я—А–Є–Љ–µ–љ—П—П —В–µ–Њ—А–µ–Љ—Г –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ –Љ—Л –Љ–Њ–ґ–µ–Љ –Ј–∞–њ–Є—Б–∞—В—М AB2=AC2+BC2-2*AC*BC*cos(∠ACB).
(√
11=4*5+4-8*√
11-24=-8*√
13=8*√
cos(∠AKC)=cos(∠ACB)=13/(8*√
–Ю—В–≤–µ—В: cos(∠AKC)=13/(8*√
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=6, BC=10, sin∠ABC=1/3. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=6, BC=10, sin∠ABC=1/3. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
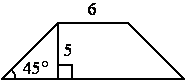 –Т —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є –Є–Ј–≤–µ—Б—В–љ—Л –≤—Л—Б–Њ—В–∞, –Љ–µ–љ—М—И–µ–µ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ –Є —Г–≥–Њ–ї –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є. –Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–µ–µ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ.
–Т —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–є —В—А–∞–њ–µ—Ж–Є–Є –Є–Ј–≤–µ—Б—В–љ—Л –≤—Л—Б–Њ—В–∞, –Љ–µ–љ—М—И–µ–µ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ –Є —Г–≥–Њ–ї –њ—А–Є –Њ—Б–љ–Њ–≤–∞–љ–Є–Є. –Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–µ–µ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ.
 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ –Ї–≤–∞–і—А–∞—В–∞, —А–∞–≤–µ–љ 16√
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ –Ї–≤–∞–і—А–∞—В–∞, —А–∞–≤–µ–љ 16√
 –Э–∞ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–∞–њ–µ—Ж–Є–Є ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є AD –Є BC –≤—Л–±—А–∞–ї–Є –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Г—О —В–Њ—З–Ї—Г E . –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —Б—Г–Љ–Љ–∞ –њ–ї–Њ—Й–∞–і–µ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ BEC –Є AED —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ–ї–Њ—Й–∞–і–Є —В—А–∞–њ–µ—Ж–Є–Є.
–Э–∞ —Б—А–µ–і–љ–µ–є –ї–Є–љ–Є–Є —В—А–∞–њ–µ—Ж–Є–Є ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є AD –Є BC –≤—Л–±—А–∞–ї–Є –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Г—О —В–Њ—З–Ї—Г E . –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —Б—Г–Љ–Љ–∞ –њ–ї–Њ—Й–∞–і–µ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ BEC –Є AED —А–∞–≤–љ–∞ –њ–Њ–ї–Њ–≤–Є–љ–µ –њ–ї–Њ—Й–∞–і–Є —В—А–∞–њ–µ—Ж–Є–Є.
–Ъ–Њ—Б–Є–љ—Г—Б –Њ—Б—В—А–Њ–≥–Њ —Г–≥–ї–∞ –Р —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–µ–љ 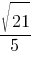 . –Э–∞–є–і–Є—В–µ sinA.
. –Э–∞–є–і–Є—В–µ sinA.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: