
 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
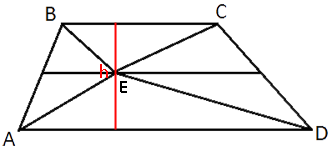 Проведем через точку E
высоту
трапеции h.
Проведем через точку E
высоту
трапеции h.
Высота h делится точкой E пополам, т.к. располагается на
средней линии, а средняя линия делит стороны трапеции пополам.
Таким образом получается, что высота обоих треугольников равна h/2.
Площадь треугольника равна половине произведения высоты на основание треугольника.
Площадь трапеции равна произведению полусуммы оснований на высоту.
SBEC=(h/2)*BC/2
SAED=(h/2)*AD/2
SBEC+SAFD=(h/2)*BC/2+(h/2)*AD/2=(h/2)(BC+AD)/2=(h*(BC+AD)/2)/2=SABCD/2
Поделитесь решением
Присоединяйтесь к нам...
 Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
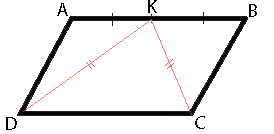 В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
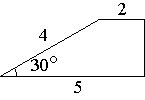 Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен
30°. Найдите площадь трапеции, если её основания равны 2 и 5.
Комментарии: