
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 39 и 42, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
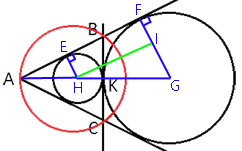 Проведем несколько отрезков:
Проведем несколько отрезков:
EH - радиус малой окружности. Он перпендикулярен AB (по
свойству касательной).
FG - радиус большой окружности. Он перпендикулярен AB (по
свойству касательной).
HG - отрезок, соединяющий центры окружностей и равный R+r, так как он проходит через точку К.
Рассмотрим треугольники AFG и AEH:
∠EAH - общий;
углы AEH и AFG - прямые.
Следовательно эти треугольники
подобны, тогда:
FG/EH=AG/AH
FG/EH=(AH+HG)/AH
42/39=(AH+R+r)/AH
42AH=39(AH+81)
42AH-39AH=3159
AH=1053
sin∠EAH=EH/AH=39/1053=1/27
AK=AH+r=1053+39=1092
AK перпендикулярен BC, т.к. AK - это продолжение большого и малого радиусов, а BC -
касательная к малой окружности (
свойство касательной). AK делит хорду BC (BC - хорда для большой окружности) пополам (по второму
свойству хорды).
Треугольник ABC -
равнобедренный, т.к. AK - и
медиана и
высота (
свойство равнобедренного треугольника).
Теперь уберем из рисунка все, что нас больше не интересует и резюмируем, что мы знаем:
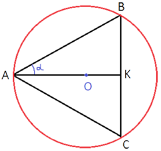 AK=1092
AK=1092
sinα=1/27
Так как AK -
биссектриса, то центр описанной окружности находится на AK.
Найдем AB.
По
теореме Пифагора:
AB2=AK2+BK2
AB2=AK2+(AB*sinα)2
AB2-AB2*sin2α=10922
AB2(1-1/272)=10922
AB2(272-1)=272*10922
AB2=272*10922/(272-1)
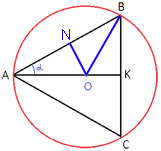 Рассмотрим треугольник AOB.
Рассмотрим треугольник AOB.
AO=OB, так как это радиусы окружности, следовательно данный треугольник
равнобедренный.
Проведем высоту ON, в
равнобедренном треугольнике она так же является и
медианой (по
свойству равнобедренного треугольника).
sinα=ON/AO => ON=AO/27
По теореме
Пифагора:
AO2=ON2+AN2
AO2=AO2/272+(AB/2)2
AO2((272-1)/272)=272*10922/(272-1)
Закончив все вычисления, получаем, что AO=546,75
Ответ: Радиус описанной окружности равен 546,75.
Поделитесь решением
Присоединяйтесь к нам...
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
 Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
 В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
 Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен
60°, а радиус окружности равен 6.
Комментарии:
(2015-05-26 10:50:39) Денис: Я нашел ошибку. ближе к концу там должно быть АВ пополам, а не просто.!!!
(2015-05-26 10:24:03) Решение не верно: при нахождении синуса угла. проверьте.
(2015-04-19 17:44:00) Администратор: Татьяна, да, не пригодился это отрезок, изначально решение было немного другим, где он был нужен...
(2015-04-19 14:09:59) Татьяна: Для чего был проведен отрезок HI?
(2014-05-29 18:57:59) Екатерина: Спасибо большое за решение