
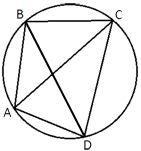 Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
∠CAD является
вписанным углом и опирается на дугу CD.
∠CBD тоже
вписанный и тоже опирается на ту же дугу CD, следовательно:
∠CAD=∠CBD=60°
∠ABD=∠ABC-∠CBD=92°-60°=32°
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
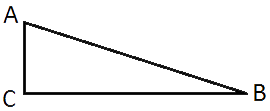 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Катеты прямоугольного треугольника равны
√
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
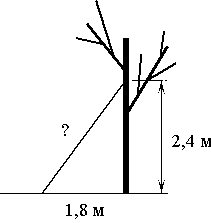 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
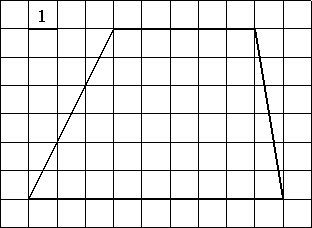 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии:
(2016-12-22 20:34:56) Администратор: Андрей, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-22 16:48:54) Андрей: четырехугольник BCDE вписан в окружность.расстояние между точками E и C равно 25, между D и C -7, между D и E -24. найти а) косинус угла CBD; б) BC, если косинус угла BCD=1/5