
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 15. Найдите BC, если AC=24.
По
теореме об описанной окружности, центр описанной окружности лежит на точке пересечения
серединных перпендикуляров сторон треугольника.
У
прямоугольного треугольника центр окрудности лежит на середине гипотенузы, так же как и в треугольнике нашей задачи, следовательно данный треугольник
прямоугольный.
Следовательно, можно применить
теорему Пифагора:
AB2=BC2+AC2
AB - диаметр окружности, так как проходит через центр.
Тогда AB=2*R=2*15=30.
302=BC2+242
900=BC2+576
BC2=900-576=324
BC=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
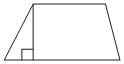 Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
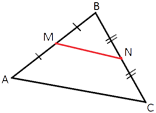 Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=42. Найдите MN.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
Комментарии: