Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
∠ADC=180°-∠BCD=180°-120°=60° (так как это внутренние односторонние углы)
∠DAB=180°-∠ABC=180°-30°=150° (так как это внутренние односторонние углы)
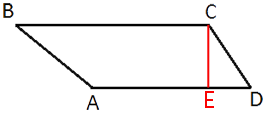Проведем высоту CE, как показано на рисунке.
Треугольник CDE - прямоугольный.
Тогда по определению синуса:
sin∠CDE=EC/CD
sin60°=EC/25
EC=25*sin60°=25*√
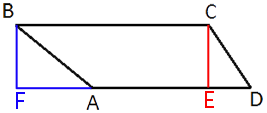Проведем высоту BF.
BF=CE=25*√
∠BAF - смежный углу BAD, следовательно:
∠BAF=180°-∠BAD=180°-150°=30°
По определению синуса:
sin∠BAF=BF/AB
sin30°=25*√
AB=25√
Ответ: AB=25√
Поделитесь решением
Присоединяйтесь к нам...
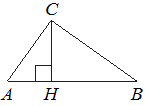На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
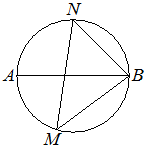На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
Найдите площадь треугольника, изображённого на рисунке.
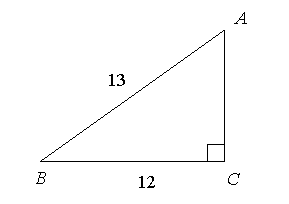Найдите площадь треугольника, изображённого на рисунке.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-09 21:40:48) Администратор: У параллелограмма противоположные стороны параллельны, а здесь параллельна только одна пара сторон, поэтому это трапеция.
(2017-01-09 18:15:30) : тут же параллелограмм нарисован,а в задаче трапеция
(2014-11-29 23:17:26) Администратор: Денис, думаю, да.
(2014-11-29 21:06:37) Денис: Это часть С ? если ответ такой?