
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ491 –Є–Ј 1087 |
 –Ґ–Њ—З–Ї–∞ H —П–≤–ї—П–µ—В—Б—П –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ –≤—Л—Б–Њ—В—Л BH, –њ—А–Њ–≤–µ–і–µ–љ–љ–Њ–є –Є–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ B –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б –і–Є–∞–Љ–µ—В—А–Њ–Љ BH –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є CB –≤ —В–Њ—З–Ї–∞—Е P –Є K —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Э–∞–є–і–Є—В–µ BH, –µ—Б–ї–Є PK=13.
–Ґ–Њ—З–Ї–∞ H —П–≤–ї—П–µ—В—Б—П –Њ—Б–љ–Њ–≤–∞–љ–Є–µ–Љ –≤—Л—Б–Њ—В—Л BH, –њ—А–Њ–≤–µ–і–µ–љ–љ–Њ–є –Є–Ј –≤–µ—А—И–Є–љ—Л –њ—А—П–Љ–Њ–≥–Њ —Г–≥–ї–∞ B –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC. –Ю–Ї—А—Г–ґ–љ–Њ—Б—В—М —Б –і–Є–∞–Љ–µ—В—А–Њ–Љ BH –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є CB –≤ —В–Њ—З–Ї–∞—Е P –Є K —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Э–∞–є–і–Є—В–µ BH, –µ—Б–ї–Є PK=13.
–Т–∞—А–Є–∞–љ—В вДЦ1 (–Я—А–Є—Б–ї–∞–ї –Њ–і–Є–љ –Є–Ј –љ–∞—И–Є—Е –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї–µ–є, –Є–Љ—П –љ–µ –Є–Ј–≤–µ—Б—В–љ–Њ).
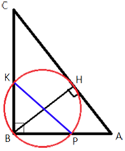 ∠KBP=90¬∞ (–њ–Њ —Г—Б–ї–Њ–≤–Є—О)
∠KBP=90¬∞ (–њ–Њ —Г—Б–ї–Њ–≤–Є—О)
–Я—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї KPB —Б –≥–Є–њ–Њ—В–µ–љ—Г–Ј–Њ–є PK –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, PK —П–≤–ї—П–µ—В—Б—П –і–Є–∞–Љ–µ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. (–њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Њ–± –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є).
KP=BH=13
–Ю—В–≤–µ—В: BH=13
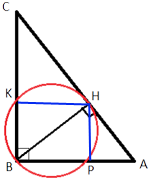 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Ї–Є KH –Є HP.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Ї–Є KH –Є HP.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –Ы—О–±–Њ–є –Ї–≤–∞–і—А–∞—В —П–≤–ї—П–µ—В—Б—П —А–Њ–Љ–±–Њ–Љ.
2) –Я—А–Њ—В–Є–≤ —А–∞–≤–љ—Л—Е —Б—В–Њ—А–Њ–љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –ї–µ–ґ–∞—В —А–∞–≤–љ—Л–µ —Г–≥–ї—Л.
3) –І–µ—А–µ–Ј –ї—О–±—Г—О —В–Њ—З–Ї—Г, –ї–µ–ґ–∞—Й—Г—О –≤–љ–µ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Љ–Њ–ґ–љ–Њ –њ—А–Њ–≤–µ—Б—В–Є –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї —Н—В–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
 –Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, AC=21, MN=14. –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–∞ 27. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ MBN.
–Я—А—П–Љ–∞—П, –њ–∞—А–∞–ї–ї–µ–ї—М–љ–∞—П —Б—В–Њ—А–Њ–љ–µ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —Б—В–Њ—А–Њ–љ—Л AB –Є BC –≤ —В–Њ—З–Ї–∞—Е M –Є N —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, AC=21, MN=14. –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–љ–∞ 27. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ MBN.
 –Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ –° —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ –° —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–≥–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
 –Э–∞ —Б—В–Њ—А–Њ–љ–µ –Р–° —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–Т–° –≤—Л–±—А–∞–љ—Л —В–Њ—З–Ї–Є D –Є E —В–∞–Ї, —З—В–Њ —Г–≥–ї—Л –РDB –Є BEC —А–∞–≤–љ—Л (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Ю–Ї–∞–Ј–∞–ї–Њ—Б—М, —З—В–Њ –Њ—В—А–µ–Ј–Ї–Є A–Х –Є CD —В–Њ–ґ–µ —А–∞–≤–љ—Л. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Р–Т–° вАФ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
–Э–∞ —Б—В–Њ—А–Њ–љ–µ –Р–° —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–Т–° –≤—Л–±—А–∞–љ—Л —В–Њ—З–Ї–Є D –Є E —В–∞–Ї, —З—В–Њ —Г–≥–ї—Л –РDB –Є BEC —А–∞–≤–љ—Л (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –Ю–Ї–∞–Ј–∞–ї–Њ—Б—М, —З—В–Њ –Њ—В—А–µ–Ј–Ї–Є A–Х –Є CD —В–Њ–ґ–µ —А–∞–≤–љ—Л. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Р–Т–° вАФ —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
 –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 28, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 28, –∞ –Њ—Б—В—А—Л–є —Г–≥–Њ–ї —А–∞–≤–µ–љ 60¬∞. –Т—Л—Б–Њ—В–∞ —А–Њ–Љ–±–∞, –Њ–њ—Г—Й–µ–љ–љ–∞—П –Є–Ј –≤–µ—А—И–Є–љ—Л —В—Г–њ–Њ–≥–Њ —Г–≥–ї–∞, –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г –љ–∞ –і–≤–∞ –Њ—В—А–µ–Ј–Ї–∞. –Ъ–∞–Ї–Њ–≤—Л –і–ї–Є–љ—Л —Н—В–Є—Е –Њ—В—А–µ–Ј–Ї–Њ–≤?
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2019-09-05 10:22:32) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ю–ї—М–≥–∞, –љ–µ –Њ—З–µ–љ—М –њ–Њ–љ—П—В–љ–Њ, —З—В–Њ –Т—Л —Е–Њ—В–µ–ї–Є —Б–Ї–∞–Ј–∞—В—М. –Э–∞–њ–Є—И–Є—В–µ, –њ–Њ–ґ–∞–ї—Г–є—Б—В–∞, –њ–Њ–њ–Њ–і—А–Њ–±–љ–µ–є.
(2019-09-04 16:31:29) –Ю–ї—М–≥–∞: –Т –і–∞–љ–љ–Њ–є –Ј–∞–і–∞—З–µ –љ—Г–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М –і–≤–∞ —А–µ—И–µ–љ–Є—П –љ–∞ 1 –±–∞–ї–ї –Є –љ–∞ 0 –±–∞–ї–ї–Њ–≤ –Ї–∞–Ї –≤ –Ю–У–≠, –Я–Ю–Ф–І–Х–†–Ъ–Э–£–Т –Я–Ю–У–†–Х–®–Э–Ю–°–Ґ–Ш –Ю–С–Ю–°–Э–Ю–Т–Р–Ґ–ђ –Т–Ђ–°–Ґ–Р–Т–Ы–Х–Э–Э–Ђ–Х –С–Р–Ы–Ы–Ђ