
 В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
По
определению: sinA=BC/AB => BC=AB*sinA=AB*7/17
По
теореме Пифагора:
AB2=BC2+AC2
AB2=(AB*7/17)2+(4√
AB2-(AB*7/17)2=16*15
AB2(1-(7/17)2)=240
AB2(289/289-49/289)=240
AB2*240/289=240
AB2=289
AB=17
Ответ: AB=17
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
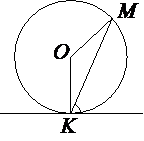 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.
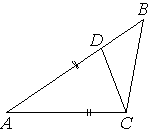 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
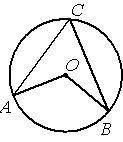 Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
 Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 170 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 340 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Комментарии:
(2015-05-24 20:34:29) Администратор: Катя, мы AB2 вынесли за скобки.
(2015-05-24 20:20:41) Катя: почему на шестой строке в решении написано 1 вместо АВ? Поясните решение на шестой строчке)