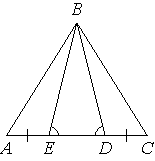
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
1) По условию задачи /BED=/EDB, следовательно треугольник BDE - равнобедренный (по
свойству). По
определению равнобедренного треугольника BE=BD.
Смежные углы для /BED и /EDB тоже равны, /BDC=/BEA.
2) Рассмотрим треугольники ABE и CBD.
AE=CD (по условию),
BE=BD (согласно п.1),
/AEB=/CDB (из п.1),
следовательно эти треугольники равны (по
первому признаку равенства треугольников), а это значит, что BA=BC. Следовательно треугольник ABC - равнобедренный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
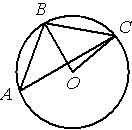Точка О – центр окружности, /BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).
В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: