В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
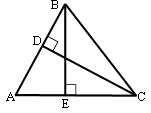Пусть AB - сторона длиной 16, а AC - сторона длиной 2.
Задачу легко решить через площадь треугольника.
Площадь треугольника равна половине произведения
высоты на сторону, к которой
высота проведена. Следовательно:
S=AB*CD/2=16*1/2=8
Так же: S=AC*BE/2
8=2*BE/2
16=2*BE
BE=8
Ответ: 8
Поделитесь решением
Присоединяйтесь к нам...
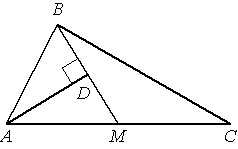Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
Точка H является основанием высоты
BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: